"Competitive Programming is a Bad Word" - that's how I started these notes. My self-esteem had decreased by 69% after the first AlgoLab lesson, so I decided to (cry and) explain the key concepts behind every ADS or Competitive Programming textbook.
This post is basically my journey through the prerequisites for AlgoLab at ETH, covering algorithmic design methods, data structures, and graph algorithms. It's raw, honest, and filled with the kind of notes I wish I had when starting out.
The Prerequisites That Scared Me
Here's what AlgoLab expects you to know (spoiler: it's a lot):
Algorithmic Design Methods
- Greedy: Minimum spanning tree (Kruskal and Prim)
- Divide and Conquer: Mergesort, quicksort, convex hull
- Dynamic Programming: Longest increasing subsequence, knapsack, matrix multiplication
- Backtracking and Recursion: Maximum independent set, 8-Queens problem
Data Structures
- Basic: Array, list, stack, queue, hash table, binary search tree, bitmask
- Priority Queues: Binary heap
- Union Find: With path compression heuristic
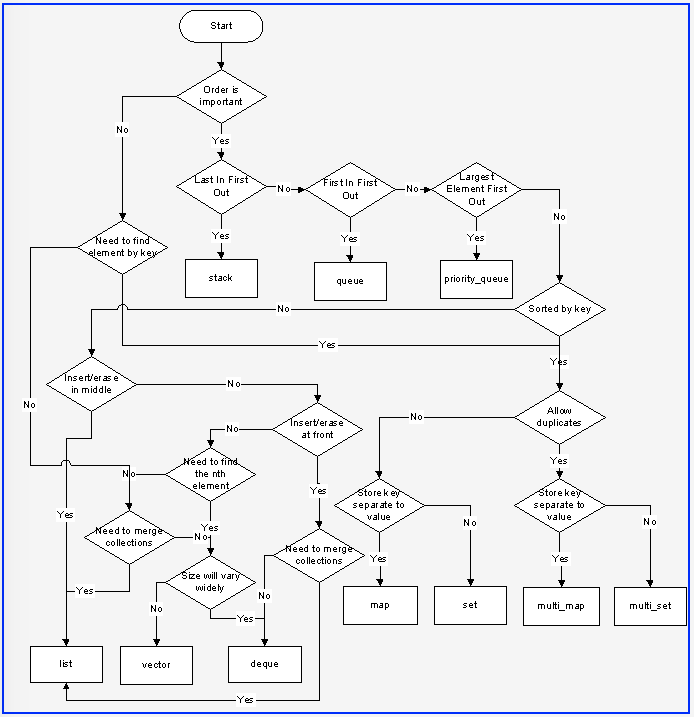
Data Structures Selection
One of the most valuable things I learned was this decision flowchart for choosing the right data structure. It's been a lifesaver in competitive programming:
Graphs: The Beast I Had to Tame
I started with graphs because it's the last data structure I didn't know well. Here's what I learned:
A graph is simply a way of encoding pairwise relationships among a set of objects: it consists of a collection V of nodes and a collection E of edges, each of which "joins" two of the nodes.
Graph Representations
There are three main ways to represent graphs, each with trade-offs. Here are some visual examples:
Visual Example: Graph with Different Representations
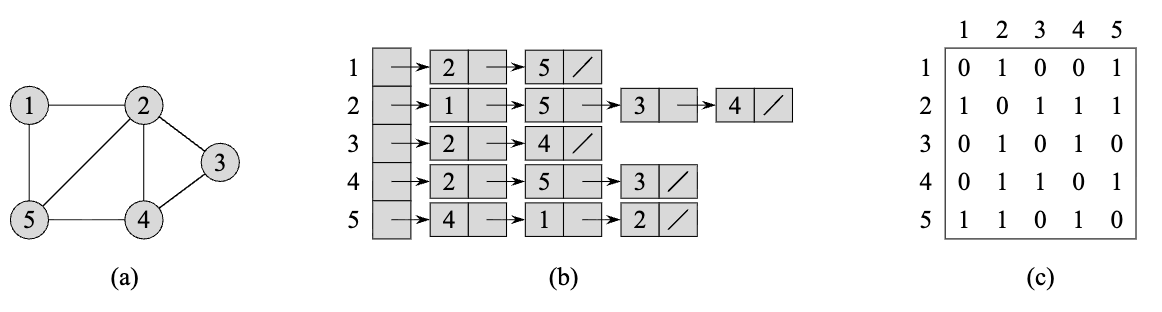
The same graph shown with (a) visual representation, (b) adjacency list, and (c) adjacency matrix
Connected vs Disconnected Graphs
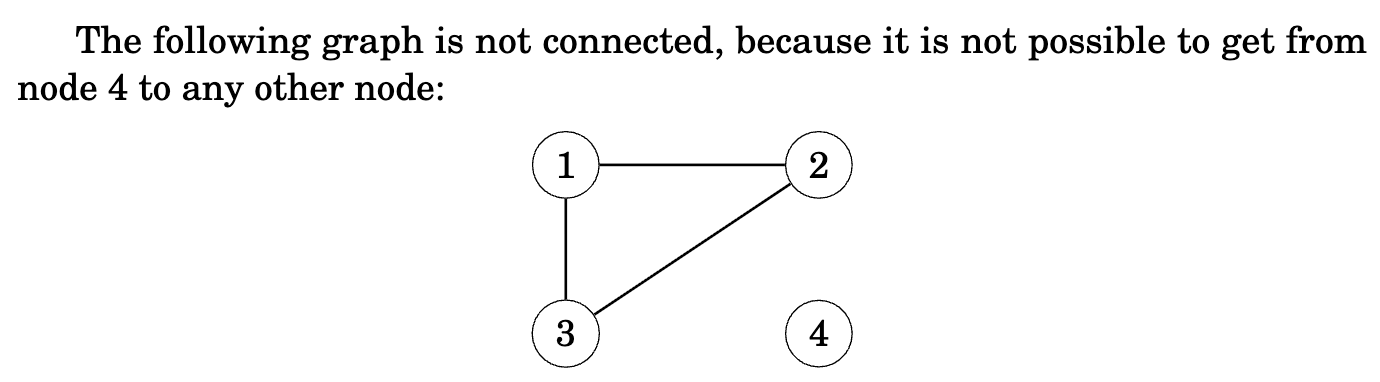
A connected graph where you can reach any node from any other node
Directed Graphs
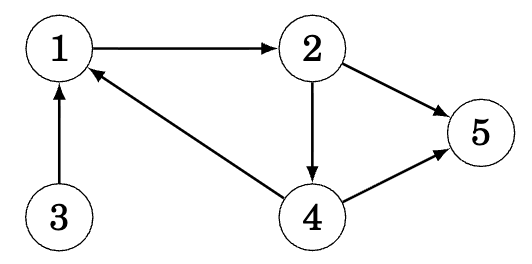
In directed graphs, edges have direction - you can only traverse them one way
Simple vs Non-Simple Graphs
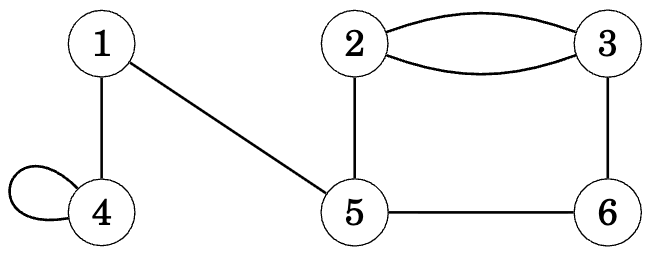
Simple graphs have no self-loops or multiple edges between the same nodes
| Method | Space | Edge Check | Find Neighbors | Best For |
|---|---|---|---|---|
| Adjacency Matrix | O(V²) | O(1) | O(V) | Dense, small graphs |
| Adjacency List | O(V+E) | O(degree) | O(degree) | Sparse graphs |
| Edge List | O(E) | O(E) | O(E) | Edge-focused algorithms |
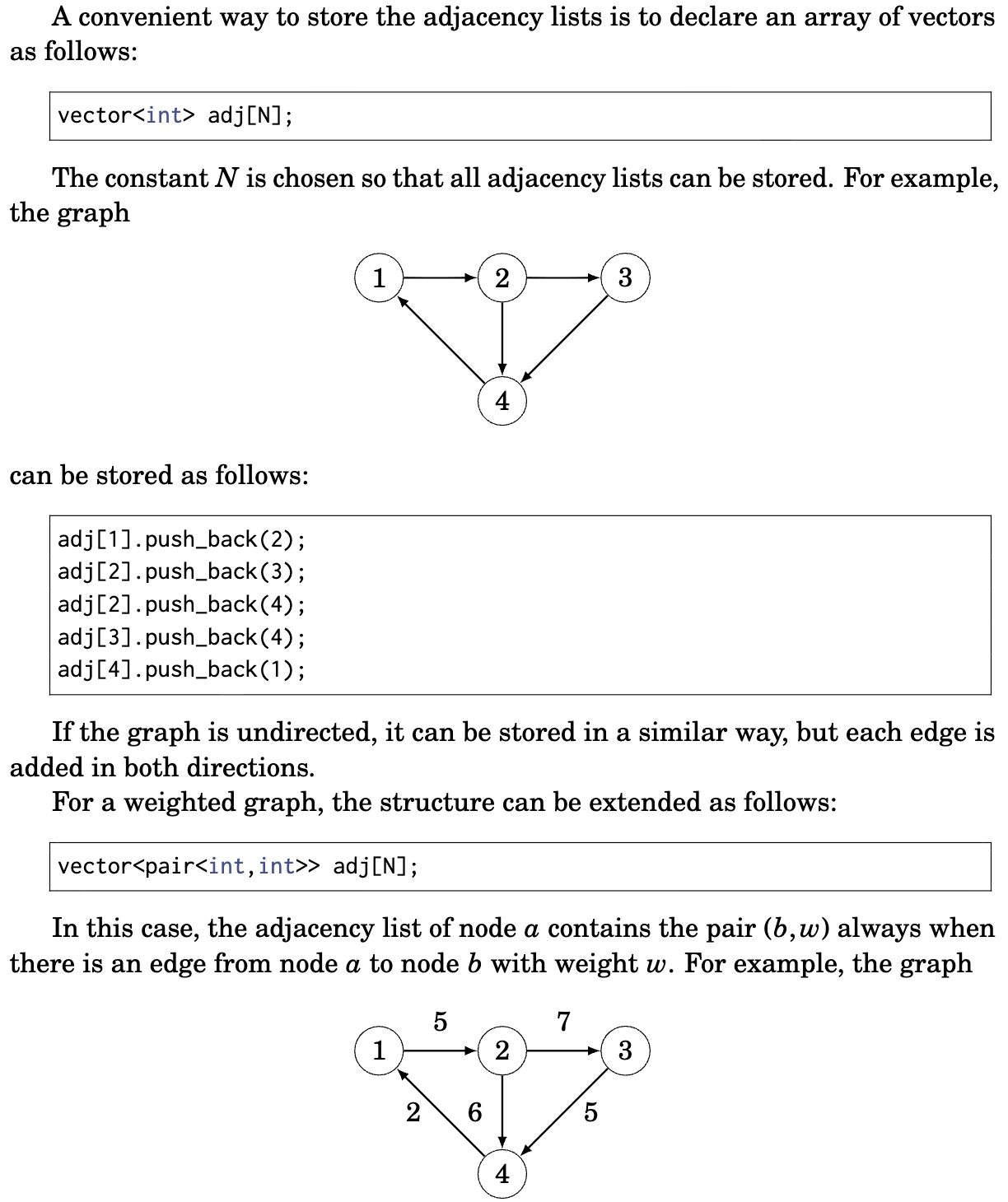
Adjacency List Implementation
Here's how to implement adjacency lists in C++. The key insight is using a vector of vectors:

A Fun Graph Moment 🐐

Sometimes graphs can look pretty cool! This one reminded me of a mountain goat.
Graph Traversal: DFS vs BFS
Depth-First Search (DFS)
The key insight with DFS is to explore neighbors before processing the node itself, and always keep track of visited nodes to avoid cycles.
void dfs(const vector<vector<int>>& graph,
int v, vector<int>& exp_lst){
if (exp_lst[v]) return;
cout << "Explored node: " << v;
exp_lst[v] = 1;
for (int node : graph[v])
dfs(graph, node, exp_lst);
}Breadth-First Search (BFS)
BFS is perfect for finding shortest paths in unweighted graphs. It processes nodes level by level using a queue.
void bfs(const vector<vector<int>>& graph,
int v, vector<int>& dist){
queue<int> q;
dist[v] = 0;
q.push(v);
while(!q.empty()){
int current = q.front(); q.pop();
for (int neighbor : graph[current])
if (dist[neighbor] == -1) {
dist[neighbor] = dist[current] + 1;
q.push(neighbor);
}
}
}Shortest Path Algorithms
Dijkstra's Algorithm
For weighted graphs with non-negative edges, Dijkstra's is the go-to. It's greedy and efficient:
// Using priority queue for efficiency
priority_queue<pair<int,int>> pq;
vector<int> dist(V, INF);
vector<bool> processed(V, false);
dist[start] = 0;
pq.push({0, start});
while (!pq.empty()) {
int u = pq.top().second; pq.pop();
if (processed[u]) continue;
processed[u] = true;
for (auto edge : graph[u]) {
int v = edge.first, weight = edge.second;
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push({-dist[v], v});
}
}
}Bellman-Ford Algorithm
When you have negative edges (but no negative cycles), Bellman-Ford is your friend. It's slower but more versatile:
vector<int> dist(V, INF);
dist[start] = 0;
// Relax edges V-1 times
for (int i = 0; i < V-1; ++i) {
for (auto [u, v, weight] : edges) {
if (dist[u] != INF && dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
}
}
}Performance Tips I Learned the Hard Way
After getting countless TLE (Time Limit Exceeded) errors, here's what actually matters:
- I/O Optimization: Always use
std::ios_base::sync_with_stdio(false) - Pass by Reference: Use
const&for large objects in function parameters - Choose the Right Data Structure: That diagram I included in my notes is gold
- Random Shuffle: Sometimes the input is adversarial -
std::random_shufflecan help
What's Next?
This is just the beginning. I still need to cover:
- Minimum Spanning Trees (Kruskal's and Prim's)
- Maximum Flow algorithms
- Dynamic Programming patterns
- More graph theory concepts
Honest Reflection
Writing these notes was therapeutic. It forced me to understand concepts deeply enough to explain them. The imposter syndrome is real in competitive programming, but breaking down complex algorithms into digestible pieces makes them less intimidating.
If you're struggling with AlgoLab or competitive programming in general, remember: we're all just trying to figure it out. The "god-tier" competitive programmers weren't born knowing Dijkstra's algorithm - they just practiced and studied systematically.
Keep coding, keep learning, and don't let a bad first lesson define your journey. 🚀